SofÐa ZafeirÐdou. Analutik GewmetrÐa. Tm ma Majhmatik n Panepist mio Patr n. Bohjhtikèc Shmei seic gia to mˆjhma. SofÐa ZafeirÐdou
|
|
|
- Ὑπατια Αξιώτης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Tm ma Majhmatik n Panepist mio Patr n Bohjhtikèc Shmei seic gia to mˆjhma Analutik GewmetrÐa Anaplhr tria Kajhg tria Pˆtra 2014
2 Οι σημειώσεις αυτές γραφτηκαν για τις ανάγκες του μαθήματος Αναλυτική Γεωμετρία Η επιλογή των ασκήσεων για το μέρος της Γραμμικής Άλγεβρας έγινε από την Επιστημονική Συνεργάτιδα Ελένη Πετροπούλου Οι διορθώσεις του κειμένου πραγματοποιήθηκαν από την μεταπτυχιακή φοιτήτρια Ευαγγελία Κακίου
3 Perieqìmena I Grammik 'Algebra 5 1 Πίνακες 7 11 Πράξεις με πίνακες Πολλαπλασιασμός πίνακα με πραγματικό αριθμό Πρόσθεση πινάκων Πολλαπλασιασμός γραμμής επί στήλη Πολλαπλασιασμός πινάκων 8 12 Βασικές ιδιότητες των πράξεων με πίνακες 9 13 Στοιχειώδεις μετασχηματισμοί των γραμμών του πίνακα Κλιμακωτοί πίνακες Βαθμός του πίνακα Ανάστροφος ενός πίνακα Αντίστροφος ενός τετραγωνικού πίνακα Ιδιότητες του αντίστροφου πίνακα Στοιχειώδεις πίνακες Ιδιότητες των στοιχειωδών πινάκων Γραμμική εξάρτηση γραμμών ή στηλών ενός πίνακα Κριτήρια αντιστρεψιμότητας ενός πίνακα Υπολογισμός του αντίστροφου πίνακα Ασκήσεις 17 2 Ορίζουσα του πίνακα Μεταθέσεις Παραβάσεις μιας μετάθεσης Ορισμός της ορίζουσας ενός τετραγωνικού πίνακα Τριγωνικοί πίνακες Ελάσσονες και αλγεβρικά συμπληρώματα Ανάπτυξη μιας ορίζουσας κατά γραμμή ή κατά στήλη Ιδιότητες των οριζουσών Ανεύρεση του αντίστροφου πίνακα Προσδιορισμός του βαθμού ενός πίνακα Ασκήσεις 27 3 Επίλυση συστημάτων γραμμικών εξισώσεων Επίλυση τετραγωνικού συστήματος με τη χρήση των πινάκων Επίλυση συστήματος με απαλοιφή αγνώστων (Μέθοδος Gauss) Επίλυση συστήματος με τον κανόνα του Cramer Ομογενή συστήματα γραμμικών εξισώσεων Ασκήσεις 36 1
4 2 II Analutik GewmetrÐa 39 4 Διανυσματικοί χώροι Εφαρμοστά διανύσματα του χώρου Ελεύθερα διανύσματα Η έννοια του διανυσματικού χώρου Γραμμική εξάρτηση στοιχείων διανυσματικού χώρου Βασικές προτάσεις για την γραμμική εξάρτηση Γεωμετρική ερμηνεία της γραμμικής εξάρτησης Βαση διανυσματικού χώρου Ασκήσεις 46 5 Συστήματα συντεταγμένων Προβολές Γενικά συστήματα συντεταγμένων Εσωτερικό γινόμενο διανυσμάτων Πολικό σύστημα συντεταγμένων στο επίπεδο Πολικό σύστημα συντεταγμένων στο χώρο Ασκήσεις 55 6 Μετασχηματισμοι συστημάτων συντεταγμένων Μετασχηματισμός γενικού συστήματος συντεταγμένων Τύποι αλλαγής των συντεταγμένων Τύποι αλλαγής των συντεταγμένων στο επίπεδο Αλλαγή ορθοκανονικού συστήματος 60 7 Εξωτερικό γινόμενο και μικτό γινόμενο διανυσμάτων Προσανατολισμός του επιπέδου και του χώρου Εξωτερικό γινόμενο και μικτό γινόμενο διανυσμάτων Εξωτερικό και μικτό γινόμενα στο χώρο με ορθοκανονικό σύστημα συντεταγμένων Ασκήσεις 66 8 Ευθείες και επίπεδα στο χώρο Εξίσωση επιπέδου Σχετική θέση επιπέδων Ευθεία στο χώρο Σχετική θέση δύο ευθειών στο χώρο Απόσταση σημείου από την ευθεία και επίπεδο Απόσταση μεταξύ των ευθειών Επίπεδο στο χώρο με ορθοκανονικό σύστημα συντεταγμένων Ευθεία στο επίπεδο Ασκήσεις Ευθεία και επίπεδο στον χώρο με γενικό σύστημα συντεταγμένων Ευθεία και επίπεδο στον χώρο με ορθοκανονικό σύστημα συντεταγμένων 80 9 Επιφάνειες 2ου βαθμού Κυλινδρικές επιφάνειες Κωνικές επιφάνειες Επιφάνειες εκ περιστροφής Ελλειψοειδές Τα υπερβολοειδή 87
5 3 96 Τα παραβολοειδή Επιφάνειες δευτέρου βαθμού Ασκήσεις 90
6 4
7 Mèroc I Grammik 'Algebra 5
8
9 Kefˆlaio 1 PÐnakec Ορισμός 101 Μια απεικόνιση A : {1,, m} {1,, n} R καλείται πίνακας τύπου m n πάνω από το R Η τιμή A(i, j) της A στο (i, j) καλείται στοιχείο i-γραμμής και j-στήλης και συμβολίζεται με a ij ή με a i,j Ενας πίνακας τύπου m n έχει m γραμμές και n στήλες και παριστάνεται ως εξής a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn Ο πίνακας A με m γραμμές, n στήλες και στοιχεία a ij για συντομία γράφεται: A = (a ij ), i = 1,, m, j = 1,, n Ενας πίνακας καλείται τετραγωνικός όταν το πλήθος των γραμμών του ισούται με το πλήθος των στηλών του, έχει δηλαδή την εξής μορφή: (11) a 11 a 12 a 1n a 21 a 22 a 2n, a ij R (12) a n1 a n2 a nn Συμβολίζουμε με M m n (R) το σύνολο όλων των πινάκων τύπου m n πάνω από το R Για κάθε φυσικό αριθμό n 1 το συνόλο M n n (R) αποτελείται από τετραγωνικούς πίνακες Τα στοιχεία του συνόλου M 1 n (R) είναι της μορφής (a 11 a 12 a 1n ) και καλούνται γραμμές a 11 a 21 Τα στοιχεία του συνόλου M n 1 (R) είναι της μορφής και καλούνται στήλες Συμβολίζουμε με A i την i-γραμμή και με A j την j-στήλη του πίνακα A Αν A M m n (R), τότε a 1j A i = (a i1 a i2 a in ), A j a 2j = a mj a n1 7
10 8 11 Prˆxeic me pðnakec 111 Pollaplasiasmìc pðnaka me pragmatikì arijmì Αν λ R και A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn καλείται γινόμενο του λ επί το A, τότε ο πίνακας λ A = Για κάθε πίνακα A συμβολίζουμε λa = λ A και A = ( 1) A λa 11 λa 12 λa 1n λa 21 λa 22 λa 2n λa m1 λa m2 λa mn 112 Prìsjesh pinˆkwn Αν A, B M m n (R), A = πίνακας A + B = καλείται άθροισμα των A και B a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn και B = a 11 + b 11 a 12 + b 12 a 1n + b 1n a 21 + b 21 a 22 + b 22 a 2n + b 2n a m1 + b m1 a m2 + b m2 a mn + b mn 113 Pollaplasiasmìc gramm c epð st lh b 11 b 12 b 1n b 21 b 22 b 2n b m1 b m2 b mn b 2 Το γινόμενο της γραμμής A = (a 1 a 2 a n ) M 1 n (R) επί την στήλη B = αριθμός (δηλαδή (1 1)-πίνακας) που ορίζεται ως εξής: A B = a 1 b 1 + a 2 b a n b n b 1 b n, τότε ο M n 1(R) είναι Το γινόμενο της i-γραμμής A i = (a i1 a i2 a in ) ένος πίνακα A με n στήλες επί την j-στήλη B j = ενός πίνακα B με n γραμμές βρίσκεται από τον τύπο b 1j b 2j b nj 114 Pollaplasiasmìc pinˆkwn Αν A = τότε ο πίνακας a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn A B = A i B j = a i1 b 1j + a i2 b 2j + + a in b nj M m n(r) και B = b 11 b 12 b 1k b 21 b 22 b 2k b n1 b n2 b nk A 1 B 1 A 1 B 2 A 1 B k A 2 B 1 A 2 B 2 A 2 B k M m k(r) A m B 1 A m B 2 A m B k M n k(r),
11 9 καλείται γινόμενο των A και B Αναλυτικότερα, A B είναι ο πίνακας a 11 b 11 + a 12 b a 1n b n1 a 11 b 12 + a 12 b a 1n b n2 a 11 b 1k + a 12 b 2k + + a 1n b nk a 21 b 11 + a 22 b a 2n b n1 a 21 b 12 + a 22 b a 2n b n2 a 21 b 1k + a 22 b 2k + + a 2n b nk a m1 b 11 + a m2 b a mn b n1 a m1 b 12 + a m2 b a mn b n2 a m1 b 1k + a m2 b 2k + + a mn b nk Παραδείγματα ( ) 4 0 = = 48 8 ( ( ) x xa xb xc 2 (a b c) = y) ya yb yc ( ) ( ( ) 2 3 x 2x + 3y 3 = 4 5 y) 4x + 5y ( ) a x ( ) b y 2a + 2b + 2c 2x + 2y + 2z = a + 3b + 3c 3x + 3y + 3z c z 12 Basikèc idiìthtec twn prˆxewn me pðnakec Ο πίνακας O = M m n(r) καλείται μηδενικός πίνακας τύπου m n Δηλαδή, μηδενικός πίνακας τύπου m n είναι ο O = (a ij ) με a ij = 0 για i = 1,, m και για j = 1,, n Ο πίνακας I = M n n (R) καλείται μοναδιαίος πίνακας τύπου n n { 1, i = j Δηλαδή, μοναδιαίος πίνακας τύπου n n είναι ο I = (a ij ) με a ij = για i, j = 1,, n 0, i j Θεώρημα 121 Αν O είναι ο μηδενικός πίνακας τύπου m n, A, B, C M m n (R) και λ, µ R, τότε 1 A + B = B + A 2 (A + B) + C = A + (B + C) 3 A + O = A 4 A + ( A) = O 5 (λ + µ)a = λa + µa 6 λ(µa) = (λµ)a 7 λ(a + B) = λa + λb 8 1 A = A
12 10 Θεώρημα 122 Ο πολλαπλασιασμός των πινάκων έχει τις ακόλουθες ιδιότητες: 1 Αν A M n n (R) και I M n n (R) είναι μοναδιαίος πίνακας, τότε A I = I A = A 2 Αν A M m n (R), B M n k (R) και C M k p (R), τότε A (B C) = (A B) C 3 Αν A M m n (R) και B, C M n k (R), τότε A (B + C) = A B + A C 4 Αν A M m n (R), B M n k (R) και λ R, τότε λ(a B) = A (λb) = (λa) B 13 Stoiqei deic metasqhmatismoð twn gramm n tou pðnaka Ορισμός 131 Στοιχειώδεις μετασχηματισμοί γραμμών ενός πίνακα A καλούνται οι εξής: 1 Πολλαπλασιασμός κάποιας γραμμής με λ R \ {0} a 11 a 12 a 1n a j1 a j2 a jn a k1 a k2 a kn λa j a 11 a 12 a 1n λa j1 λa j2 λa jn a k1 a k2 a kn 2 Η πρόσθεση σε μια γραμμη του πίνακα κάποιας άλλης γραμμής πολλαπλασιασμένης με λ R \ {0} a 11 a 12 a 1n a j1 a j2 a jn a i1 a i2 a in a k1 a k2 a kn A i+λa j a 11 a 12 a 1n a j1 a j2 a jn a i1 + λa j1 a i2 + λa j2 a in + λa jn a k1 a k2 a kn 3 Αντιμετάθεση δύο γραμμών a 11 a 12 a 1n a i1 a i2 a in a j1 a j2 a jn a k1 a k2 a kn A i A j a 11 a 12 a 1n a j1 a j2 a jn a i1 a i2 a in a k1 a k2 a kn Ορισμός 132 Δύο πίνακες καλούνται γραμμοϊσοδύναμοι, όταν ο ένας προκύπτει από τον άλλον μετά την εφαρμογή πεπερασμένου πλήθους στοιχειωδών μετασχηματισμών γραμμών
13 131 KlimakwtoÐ pðnakec Μια γραμμή A i ενός πίνακα A M m n (R) καλείται μηδενική αν a ij = 0 για κάθε j = 1,, n Το πρώτο μη μηδενικό στοιχείο μιας μη μηδενικής γραμμής ενός πίνακα καλείται ηγετικό στοιχείο της γραμμής αυτής Δηλαδή, το στοιχείο a ij 0 της i-οστής γραμμής είναι ηγετικό, όταν ή j = 1 ή j 1 και a i1 = = a ij 1 = 0 Ορισμός 133 Ενας πίνακας m n καλείται κλιμακωτός, όταν έχει τις ακόλουθες ιδιότητες: 1 οι μη μηδενικές γραμμές του πίνακα προηγούνται των μηδενικών γραμμών 2 αν a 1i1, a 2i2,, a nin είναι τα ηγετικά στοιχεία, αντίστοιχα, της 1ης, 2ης,, n-στης γραμμής, τότε i 1 < i 2 < < i n Θεώρημα 134 Κάθε μη μηδενικός πίνακας είναι γραμμοϊσοδύναμος με έναν κλιμακωτό πίνακα Απόδειξη 11 Παράδειγμα A1 A3 14 Bajmìc tou pðnaka A2 2A A A Οι γραμμές A i1, A i2,, A ik είναι γραμμικώς ανεξάρτητες, όταν καμμία από αυτές δεν εκφράζεται ως γραμμικός συνδυασμός των άλλων Παραδείγματα Εστω A = Οι γραμμές A 1 = (1 2 3) και A 2 = (1 4 2) είναι γραμμικώς ανεξάρτητες, αφού A 2 λa 1 για κάθε λ R Οι γραμμές A 1, A 2, A 3 είναι γραμμικώς εξαρτημένες, αφού A 3 = 2A 1 + A Οι γραμμές του κλιμακωτού πίνακα είναι γραμμικώς ανεξάρτητες Ορισμός 142 Το μέγιστο πλήθος των γραμμικώς ανεξάρτητων γραμμών ενός πίνακα A καλείται βαθμός του A και συμβολίζεται με rank(a) Θεώρημα 143 Αν οι πίνακες A και B είναι ισοδύναμοι, τότε rank(a) = rank(b) Επειδή οι μη μηδενικές γραμμές οποιουδήποτε κλιμακωτού πίνακα είναι γραμμικώς ανεξάρτητες, από τα Θεωρήματα 134 και 143 προκύπτει ότι: Ο βαθμός ενός πίνακα A ισούται με το πλήθος των μη μηδενικών γραμμών του κλιμακωτού πίνακα γραμμοϊσοδύναμου με τον A Παράδειγμα A = A1+A3 Άρα, rank(a) = A A1 A A1 A A2 A
14 12 15 Anˆstrofoc enìc pðnaka Ο ανάστροφος ενός πίνακα A = (a ij ) τύπου m n λέγεται ο πίνακας A t = (a ji ) τύπου n m όπου a ji = a ij Δηλαδή οι i-στήλη του A t είναι η i-γραμμή του A: a 11 a 12 a 1n a 11 a 21 a m1 a 21 a 22 a 2n A = M m n(r) = A t a 12 a 22 a m2 = M n m(r) a m1 a m2 a mn a 1n a 2n a mn Παράδειγμα 151 A = ( ) = A t = Θεώρημα 152 Αν A M m n (R), τότε 1 (A t ) t = A 2 (A + B) t = A t + B t, B M m n (R) 3 (A B) t = B t A t, B M n k (R) 4 (λa) t = λa t 16 AntÐstrofoc enìc tetragwnikoô pðnaka Ενας τετραγωνικός πίνακας A M n n (R) καλείται αντιστρέψιμος όταν υπάρχει πίνακας B M n n (R) τέτοιος ώστε A B = B A = I, (13) όπου I είναι ο μοναδιαίος τετραγωνικός πίνακας τύπου n n Θεώρημα 161 Για κάθε αντιστρέψιμο πίνακα A υπάρχει μοναδικός πίνακας B για τον οποίον ισχύουν οι ισότητες (13) Για κάθε αντιστρέψιμο πίνακα A ο μοναδικός πίνακας B για τον οποίο ισχύουν οι ισότητες (13), καλείται αντίστροφος πίνακας του A και συμβολίζεται με A 1, οπότε A A 1 = A 1 A = I 161 Idiìthtec tou antðstrofou pðnaka 1 Αν οι πίνακες A, B M n n (R) είναι αντστρέψιμοι, τότε ο πίνακας A B είναι αντιστρέψιμος και (A B) 1 = B 1 A 1 2 Αν ο πίνακας A M n n (R) είναι αντστρέψιμος, τότε ο πίνακας A t είναι αντιστρέψιμος και (A t ) 1 = (A 1 ) t
15 13 17 Stoiqei deic pðnakec Ορισμός 171 Ενας τετραγωνικός πίνακας τύπου n n καλείται στοιχειώδης όταν μπορεί να προκύψει από τον μοναδιαίο πίνακα τύπου n n εφαρμόζοντας έναν στοιχειώδη μετασχηματισμο γραμμών Υπάρχουν τρείς μορφές στοιχειωδών πινάκων, κάθεμιά από τις οποίες αντιστοιχεί σε έναν στοιχειώδη μετασχηματισμό γραμμών: 1 Πολλαπλασιασμός κάποιας γραμμής του I με λ R \ {0} I = 1 i γραμμή λai λ 1 1 = I λ[i] 2 Η πρόσθεση σε μια γραμμη του I μιας άλλης γραμμής πολλαπλασιασμένης με λ R \ {0} i γραμμή 1 λ I = A i+λa j = I [i]+λ[j] 1 j γραμμή Αντιμετάθεση δύο γραμμών του I 1 1 I = 1 1 i γραμμή j γραμμή A i A j = I [i] [j] 171 Idiìthtec twn stoiqeiwd n pinˆkwn 1 Κάθε στοιχειώδης πίνακας είναι αντιστρέψιμος 2 Ο αντίστροφος πίνακας ενός στοιχειώδους πίνακα είναι στοιχειώδης 3 Το γινόμενο δύο στοιχειωδών πινάκων είναι στοιχειώδης πίνακας Θεώρημα 172 Ο πίνακας B M m n (R) προκύπτει από τον πίνακα A M m n (R) με την εφαρμογή του στοιχειώδους μετασχηματισμού γραμμών φ αν και μόνον αν B = I ϕ A, όπου I φ είναι ο στοιχειώδης πίνακας που προκύπτει από το μοναδιαίο πίνακα I M m m (R) με την εφαρμογή του φ
16 14 Παράδειγμα 171 Αν φ συμβολίζει τον στοιχειώδη μετασηματισμό γραμμών A 1 + 2A 2 (την πρόσθεση της δεύτερης γραμμής πολλαπλασιασμένης επί 2 στην πρώτη γραμμή ), τότε A = I φ A = I = φ φ = = B = I φ = B Θεώρημα 174 Ο πίνακας B M m n (R) προκύπτει από τον πίνακα A M m n (R) με την διαδοχική εφαρμογή των στοιχειωδών μετασχηματισμών γραμμών φ 1, φ 2,, φ k αν και μόνον αν B = I ϕk I ϕ2 I ϕ1 A, όπου I φi είναι ο στοιχειώδης πίνακας που προκύπτει από το μοναδιαίο πίνακα I M m m (R) με την εφαρμογή του φ i 18 Grammik exˆrthsh gramm n sthl n enìc pðnaka Θα λέμε ότι η γραμμή A i ενός πίνακα A είναι γραμμικώς συνδυασμός των γραμμών A i1, A i2,, A in, όταν A i = λ 1 A i1 + λ 2 A i2 + + λ n A in, όπου λ 1, λ 2,, λ n R Οι γραμμές ενός πίνακα A καλούνται γραμμικώς εξαρτημένες, όταν υπάρχει γραμμή του A που είναι γραμμικός συνδυασμός άλλων γραμμών Οι γραμμές ενός πίνακα A καλούνται γραμμικώς ανεξάρτητες, όταν δεν είναι γραμμικώς εξαρτημένες Ομοια ορίζεται η γραμμική εξάρτηση (ανεξαρτησία) των στηλών ενός πίνακα Παραδείγματα Οι γραμμές του A = 2 Οι στήλες του B = 3 Οι γραμμές του C = 4 Οι στήλες του D = είναι γραμμικώς εξαρτημένες, αφού A 3 = 2A 1 + 3A είναι γραμμικώς εξαρτημένες, αφού A 2 = A 1 + A 3 είναι γραμμικώς εξαρτημένες, αφού A 3 = 0 A A A 4 είναι γραμμικώς εξαρτημένες, αφού A 1 = 0 A 2 +0 A 3 +0 A 4
17 15 19 Krit ria antistreyimìthtac enìc pðnaka Θεώρημα 191 Για έναν τετραγωνικό πίνακα A M n n (R) τα εξής είναι ισοδύναμα: (a) Ο A είναι αντιστρέψιμος (b) Οι γραμμές του A είναι γραμμικώς ανεξάρτητες (c) Οι στήλες του A είναι γραμμικώς ανεξάρτητες (d) Ο A είναι γινόμενο πεπερασμένου πλήθους στοιχειωδών πινάκων (e) Ο A είναι ισοδύναμος με τον μοναδιαίο πίνακα I M n n (R) Πόρισμα 192 Ενας τετραγωνικός πίνακας που περιέχει μηδενική γραμμή ή μηδενική στήλη δεν είναι αντιστρέψιμος 191 Upologismìc tou antðstrofou pðnaka Από τα Θεωρήματα 174 και 191(e) συνεπάγεται ότι αν ένας πίνακας A M n n (R) είναι αντιστρέψιμος, τότε I = I ϕk I ϕ2 I ϕ1 A, όπου I φi είναι ο στοιχειώδης πίνακας που προκύπτει από τον μοναδιαίο πίνακα I M n n (R) με την εφαρμογή του στοιχειώδους μετασχηματισμού γραμμών φ i Πολλαπλασιάζοντας με A 1 από δεξιά και τα δύο μέλη της προηγούμενης ισότητας παίρνουμε I A 1 = I ϕk I ϕ2 I ϕ1 A A 1 A 1 = I ϕk I ϕ2 I ϕ1 I Από τα παραπάνω συμπεραίνουμε ότι αν ο I προκύπτει μετά την εφαρμογή των στοιχειωδών μετασχηματισμών γραμμών φ 1, φ 2,, φ k στον A, τότε ο A 1 προκύπτει μετά την εφαρμογή των στοιχειωδών μετασχηματισμών γραμμών φ 1, φ 2,, φ k στον I Άρα, για να βρούμε τον αντίστροφο ενός πίνακα A μπορούμε να εφαρμόσουμε τον εξής κανόνα: Αν φέρουμε τον πίνακα (A I) με τη βοήθεια των στοιχειωδών μετασχηματισμών γραμμών στη μορφή (I B), τότε B = A 1 Παραδείγματα Να βρεθεί ο αντίστροφος πίνακας του A = ( Εφαρμόζουμε διαδοχικούς στοιχειώδεις μετασχηματισμούς γραμμών στον πίνακα (A I 2 ) έτσι ώστε ο A του (A I 2 ) να μετασχηματιστεί στον πίνακα I 2, τότε ο I 2 του (A I 2 ) θα μετασχηματιστεί στον A 1 (A I 2 ) = ( ) A 2 2A 1 ( ) ) A 1+3A 2 ( ) ( 1 2 A1 1 0 A ) = (I 2 A 1 ) Συνεπώς, ( ) A =
18 16 2 Να βρεθεί ο αντίστροφος πίνακας του A = Εφαρμόζουμε διαδοχικούς στοιχειώδεις μετασχηματισμούς γραμμών στον πίνακα (A I 3 ) έτσι ώστε ο A του (A I 3 ) να μετασχηματιστεί στον πίνακα I 3, τότε ο I 3 του (A I 3 ) θα μετασχηματιστεί στον A (A I 3 ) = A1 A A A Συνεπώς, A 3+A 2 A 1 3A A2 A 1 = A2 A = (I 3 A 1 )
19 Ask seic 1 Να βρεθεί ο πίνακας B που πρέπει να προστεθεί στον πίνακα A = ώστε να προκύψει μοναδιαίος πίνακας 2 Να βρεθούν οι πίνακες A + B και A B, όταν ( (i) A = (ii) A = ) ( , B = a a 2+b 1 a 3+c a 2+b 1 b 2 b 3+c a 3+c 1 b 3+c c 3, B = 3 Να βρεθούν οι ανάστροφοι των πινάκων: ( ), ( ) 1 6 3, ) a 0 2 b 1 a 3 c a2 b1 b c 2 2 a3 c1 b 3 c , 3 x a b a y c, b c z 4 Ενας τετραγωνικός πίνακας A καλείται συμμετρικός, όταν A = A t (i) Να δοθεί παράδειγμα ενός 3 3 συμμετρικού πίνακα (ii) Να βρεθούν οι τιμές του x για τις οποίες ο πίνακας είναι 2 1 5x x Ενας τετραγωνικός πίνακας A καλείται αντισυμμετρικός όταν A t = A (i) Να δοθεί παράδειγμα ενός 3 3 αντισυμμετρικού πίνακα 0 a b a 0 c b c 0 συμμετρικός (ii) Να αποδειχθεί ότι κάθε τετραγωνικός πίνακας μπορεί να γραφεί ως άθροισμα ενός συμμετρικού και ενός αντισυμμετρικού πίνακα 6 Δίνονται οι πίνακες A = ( ) ( 1 3, B = 4 2 ), C = (i) Ποια από τα γινόμενα A 2, AC, DA, AD, D 2, DC, CD, C 2 είναι δυνατά; (ii) Να διερευνηθεί αν οι πίνακες AB και BA είναι ίσοι Να βρεθεί ο πίνακας A + A 2 + I, αν A = Να βρεθούν τα γινόμενα των πινάκων:, D = ( ( ) ( ) a a11 a (x y) 12 x 11 a 12 a 1 x, (x y 1) a a 12 a 22 y 12 a 22 a 2 y a 1 a 2 a 0 1 )
20 18 9 Για τον πίνακα A = Να αναχθούν σε κλιμακωτή μορφή οι πίνακες: (i) , (ii) να βρεθεί ο πίνακας B για τον οποίο AB =, (iii) a b c a 2 b 2 c Να προσδιοριστούν οι βαθμοί των πινάκων: , , Να αποδειχθεί ότι ο πίνακας είναι αντίστροφος του πίνακα Για τον πίνακα A = να βρεθούν οι πίνακες (A t ) 1 και ( A 1) t ( ) ( ) 8 3 a b 14 Να βρεθούν οι αντίστροφοι των πινάκων:,, 1 2 c d 15 Να σχολιαστεί γιατί οι παρακάτω πίνακες δεν είναι αντιστρέψιμοι: ( ), , , ( ) Να παρασταθεί ο πίνακας A = ως γινόμενο στοιχειωδών πινάκων 3 4 9/5 2/5 4/5 1/5 2/5 1/5 12/5 1/5 7/5, a 2a + 3x x b 2b + 3y y c 2c + 3z z Λύση A = ( ) ( A 2 3A ϕ1 0 2 ) ( 1 2 A2 1 2 ϕ2 0 1 Από το Θεώρημα 174: I = I ϕ3 I ϕ2 I ϕ1 A Επομένως A = I ϕ 1 1 ( ) ) 1 0 Άρα, I = 0 1 ( ) 1 0 I = 0 1 ( ) 1 0 I = 0 1 A = ( A 2+3A 1 ϕ 1 1 2A 2 ϕ 1 2 A 1+2A 2 ϕ 1 3 ( ( 1 ) ( 1 2 ) 0 1 ) ( ) ( A 1 2A ϕ3 0 1 I ϕ 1 2 = I ϕ 1 1 = I ϕ 1 2 = I ϕ 1 3 ) ( ) I ϕ 1 3 ) = I
21 Kefˆlaio 2 OrÐzousa tou pðnaka Στο Κεφάλαιο αυτό για κάθε φυσικό αριθμό n 1 θα ορίσουμε μια απεικόνιση det : M n n (R) R, με επιθυμητές ιδιότητες Η απεικόνιση det σε κάθε τετραγωνικό πίνακα A αντιστοιχεί έναν πραγματικό αριθμό την ορίζουσα του A 21 Metajèseic Εστω {p 1, p 2, p n } ένα πεπερασμένο σύνολο Κάθε ένα-προς -ένα και επί απεικόνιση µ : {p 1, p 2,, p n } {p 1, p 2,, p n } καλείται μετάθεση Η μετάθεση µ συμβολίζεται με πίνακα ( ) p1 p µ = 2 p n µ(p 1 ) µ(p 2 ) µ(p n ) Η αντίστροφη της μετάθεσης µ είναι η μετάθεση ( ) µ 1 µ(p1 ) µ(p = 2 ) µ(p n ) p 1 p 2 p n ( ) ( p1 p Αν µ = 2 p n p1 p και ν = 2 p n µ(p 1 ) µ(p 2 ) µ(p n ) ν(p 1 ) ν(p 2 ) ν(p n ) είναι η μετάθεση ( ) p ν µ = 1 p 2 p n ν(µ(p 1 )) ν(µ(p 2 )) ν(µ(p n )) Το πλήθος των μεταθέσεων ένος συνόλου με n στοιχεία ισούται με n! ), τότε γινόμενο µ επί ν Θα περιοριστούμε στις μεταθέσεις των πεπερασμένων συνόλων φυσικών αριθμών της μορφής S n = {1, 2,, n} Θα συμβολίζουμε με S n το σύνολο όλων των μεταθέσεων του S n ( ) 1 2 n Η μετάθεση 1 n = του S 1 2 n n καλείται ταυτοτική μετάθεση του S n Μια μετάθεση α : S n S n καλείται αντιμετάθεση αν υπάρχουν i, j S n τέτοια ώστε α(i) = j, α(j) = i και α(k) = k για k S n \ {i, j} Μια αντιμετάθεση των στοιχείων i, j μπορεί να παρασταθεί ως εξής: ( ) 1 i j n α(i, j) = 1 j i n 19
22 20 Παραδείγματα Ορίζουμε τη μετάθεση µ : {1, 2, 3, 4} {1, 2, 3, 4} ως εξής: µ(1) = 2, µ(2) = 4, µ(3) = 1, µ(4) = 3 Τότε 2 Αν µ = ( µ = ( µ(1) µ(2) µ(3) µ(4) ) και ν = ν µ = ( ( ), τότε ) = ( ) ( , µ ν = ) ) 3 Το πλήθος των μεταθέσεων του S 3 = {1, 2, 3} είναι 3! = 6, οι οποίες είναι οι εξής: 4 Αν ω = ( ( ) ( ) µ 1 =, µ =, µ = ( ) ( ) µ 4 =, µ =, µ = ) ( 1 2 3, τότε ω 1 = S 3 = {µ 1, µ 2, µ 3, µ 4, µ 5, µ 6 } ) Επίσης ω ω 1 = ( ) ( ) Οι αντιμεταθέσεις του S 3 είναι:, Parabˆseic miac metˆjeshc ( ( ( ( ) ), ), ) = 1 3 Εστω i, j S n = {1,, n} και i < j Το ζευγος (i, j) καλείται παράβαση μιας μετάθεσης µ S n, όταν µ(i) > µ(j) Συμβολίζουμε με π(µ) το πλήθος των παραβάσεων της μετάθεσης µ Η µ καλείται άρτια μετάθεση (αντίστοιχα, περιττή μετάθεση), όταν ο αριθμός π(µ) είναι άρτιος (αντίστοιχα, περιττός) Παράδειγμα Το πλήθος των παραβάσεων της ταυτοτικής μετάθεσης 1 n = ( 1 2 n 1 2 n ) είναι μηδέν ( ) Αν ϕ =, τότε το σύνολο των παραβάσεων της ϕ είναι {(1, 3), (2, 3)} Επομένως, π(ϕ) = Η μετάθεση ϕ είναι άρτια 3 Αν µ = ( ), τότε το σύνολο των παραβάσεων της µ είναι {(1, 3), (2, 3), (2, 4)} Επομένως, π(µ) = 3 Η μετάθεση µ είναι περιττή
23 21 22 Orismìc thc orðzousac enìc tetragwnikoô pðnaka Ορισμός 221 Για κάθε τετραγωνικό πίνακα a 11 a 12 a 1n a 21 a 22 a 2n A = M n n(r) a n1 a n2 a nn ο αριθμός det(a) = ( 1) π(µ) a 1µ(1) a 2µ(2) a nµ(n) µ S n καλείται ορίζουσα του A Η απεικόνιση det : M n n (R) R, η οποία σε κάθε πίνακα A M n n (R) αντιστοιχίζει την ορίζουσα του A, καλείται ορίζουσιακή Η ορίζουσα ενός πίνακα A συμβολίζεται και με A Παραδείγματα Εστω A = ( ) a11 a 12 a 21 a 22 Για S 2 = {1, 2}, το σύνολο των μεταθέσεων είναι S 2 = {µ 1, µ 2 }, όπου Εχουμε π(µ 1 ) = 0 και π(µ 2 ) = 1 Επομένως ( ) ( ) µ 1 =, µ = 2 1 det(a) = ( 1) π(µ1) a 1µ1(1)a 2µ1(2) + ( 1) π(µ2) a 1µ2(1)a 2µ2(2) = a 11 a 22 a 12 a 21 2 Εστω A = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 Για S 3 = {1, 2, 3}, το σύνολο των μεταθέσεων είναι S 3 = {µ 1, µ 2, µ 3, µ 4, µ 5, µ 6 }, όπου µ 1 = µ 4 = ( ( ) ( 1 2 3, µ 2 = ) ( 1 2 3, µ 5 = ) ( 1 2 3, µ 3 = ) ( 1 2 3, µ 6 = ), ) Εχουμε π(µ 1 ) = 0 και π(µ 2 ) = 2, π(µ 3 ) = 2, π(µ 4 ) = 3, π(µ 5 ) = 1, π(µ 6 ) = 1 Επομένως, det(a) = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 a 13 a 22 a 31 a 11 a 23 a 32 a 12 a 21 a 33
24 TrigwnikoÐ pðnakec Εστω A = (a ij ) M n n (R) ένας τετραγωνικός πίνακας Ο A = (a ij ) καλείται διαγώνιος όταν a ij = 0 για κάθε i j Ο A = (a ij ) καλείται άνω τριγωνικός όταν a ij = 0 για κάθε i > j Ο A = (a ij ) καλείται κάτω τριγωνικός όταν a ij = 0 για κάθε i < j Οι άνω τριγωνικοί και οι κάτω τριγωνικοί πίνακες καλούνται τριγωνικοί πίνακες Οι τριγωνικοί πίνακες παριστάνονται ως εξής: a a 22 0 διαγώνιος πίνακας 0 0 a nn a 11 a 12 a 1n 0 a 22 a 2n άνω τριγωνικός πίνακας 0 0 a nn a a 21 a 22 0 κάτω τριγωνικός πίνακας a n1 a n2 a nn Τα στοιχεία a 11, a 22,, a nn ενός πίνακα A M n n (R) καλούνται διαγώνια Θεώρημα 223 Η ορίζουσα κάθε τριγωνικού πίνακα (διαγώνιου, άνω τριγωνικού, κάτω τριγωνικού) ισούται με το γινόμενο των διαγώνιων στοιχείων του Επομένως, a a 11 a 12 a 1n a a a 22 a 2n a 21 a 22 0 = = = a 11 a 22 a nn 0 0 a nn 0 0 a nn a n1 a n2 a nn 23 Elˆssonec kai algebrikˆ sumplhr mata Θεωρούμε έναν τετραγωνικό πίνακα a 11 a 12 a 1n a 21 a 22 a 2n A = M n n(r) a n1 a n2 a nn Ο πίνακας που προκύπτει από τον πίνακα A όταν διαγράψουμε την i-γραμμή και την j-στήλη καλείται ελάσσονας του a ij και συμβολίζεται με M j i Ο αριθμός A ij = ( 1) i+j det(m j i ) καλείται αλγεβρικό συμπλήρωμα του στοιχείου a ij
25 23 Παραδείγματα 231 ( ) a11 a 1 A = 12 = M a 21 a 1 1 = a 22, M1 2 = a 21, M2 1 = a 12, M2 2 = a 11 = 22 A 11 = ( 1) 1+1 det(m 1 1 ) = a 22, A 12 = ( 1) 1+2 det(m 2 1 ) = a 21, A 21 = ( 1) 2+1 det(m2 1 ) = a 12, A 22 = ( 1) 2+2 det(m2 2 ) = a 11 a 11 a 12 a 13 ( ) 2 A = a 21 a 22 a 23 = M 2 a11 a 2 = 13 = A a a 31 a 32 a 31 a 22 = ( 1) 2+2 det(m2 2 ) = (a 11 a 33 a 13 a 31 ) Anˆptuxh miac orðzousac katˆ gramm katˆ st lh Θεώρημα 241 Η ορίζουσα ενός πίνακα A M n n (R) ισούται με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε γραμμής επί τα αλγεβρικά τους συμπληρώματα, δηλαδή det(a) = n a ij A ij = a i1 A i1 + + a in A in, i = 1,, n j=1 Θεώρημα 242 Η ορίζουσα ενός πίνακα A M n n (R) ισούται με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε στήλης επί τα αλγεβρικά τους συμπληρώματα, δηλαδή det(a) = n a ij A ij = a 1j A 1j + + a nj A nj, j = 1,, n i=1 Με τη βοήθεια των πινάκων M j i που προκύπτουν με τη διαγραφή της i-γραμμής και j-στήλης ενός πίνακα A τύπου n n, παίρνουμε: την ανάπτυξη της ορίζουσας του A κατά i-γραμμή det(a) = την ανάπτυξη της ορίζουσας του A κατά j-στήλη n ( 1) i+j a ij M j i, j=1 det(a) = n ( 1) i+j a ij M j i i=1 a 11 a 12 a 13 Παραδείγματα 241 Εστω A = a 21 a 22 a 23 a 31 a 32 a 33 1 Αναπτύσσοντας την ορίζουσα του A κατά τα στοιχεία της 1ης γραμμής παίρνουμε det(a) = ( 1) 1+1 a a 22 a a 32 a 33 + a ( 1)1+2 a 21 a a 31 a 33 + a ( 1)1+3 a 21 a a 31 a 32 = a = a 22 a a 32 a 33 a 12 a 21 a 23 a 31 a 33 + a 13 a 21 a 22 a 31 a 32 2 Αναπτύσσοντας την ορίζουσα του A κατά τα στοιχεία της 2ης στήλης παίρνουμε det(a) = ( 1) 1+2 a a 21 a a 31 a 33 + a ( 1)2+2 a 11 a a 31 a 33 + a ( 1)3+2 a 11 a a 21 a 23 a = a 21 a a 31 a 33 + a 22 a 11 a 13 a 31 a 33 a 32 a 11 a 13 a 21 a 23 =
26 24 25 Idiìthtec twn orizous n 1 Η ορίζουσα ενός τετραγωνικού πίνακα αλλάζει πρόσημο κατά την αντιμετάθεση δύο γραμμών (αντίστοιχα, δύο στηλών): a j1 a j2 a jn a i1 a i2 a in = a i1 a i2 a in a j1 a j2 a jn a 1i a 1j a 2i a 2j a ni a nj = a 1j a 1i a 2j a 2i a nj a ni 2 Αν σε μια γραμμή (αντίστοιχα, στήλη) ενός πίνακα προστεθεί μια άλλη γραμμή (αντίστοιχα, στήλη )του ίδιου πίνακα πολλαπλασιασμένη με έναν αριθμό λ, τότε ο πίνακας που προκύπτει έχει την ίδια ορίζουσα: a i1 a i2 a in a j1 a j2 a jn = a i1 + λa j1 a i2 + λa j2 a in + λa jn a j1 a j2 a jn a 1j a 1i a 2j a 2i a nj a ni = a 1i a 1j + λa 1i a 2i a 2j + λa 2i a ni a nj + λa ni 3 Αν μια γραμμή (αντίστοιχα, στήλη) ένος πίνακα A πολλαπλασιαστεί με έναν αριθμό λ 0, τότε προκύπτει πίνακας με ορίζουσα λ A : a 11 a 12 a 1n a i1 a i2 a in a n1 a n2 a nn = 1 λ a 11 a 12 a 1n λa i1 λa i2 λa in a n1 a n2 a nn a 11 a 1i a 1n a 21 a 2i a 2n a n1 a ni a nn = 1 λ a 11 λa 1j a 1n a 21 λa 2n a 2n a n1 λa nj a nn
27 25 4 a 11 a 12 a 1n a 11 a 12 a 1n a 11 a 12 a 1n a i1 + a i1 a i2 + a i2 a in + a in = a i1 a i2 a in + a i1 a i2 a in a n1 a n2 a nn a n1 a n2 a nn a n1 a n2 a nn a 11 a 1i + a 1i a 1n a 21 a 2i + a 2i a 2n a n1 a ni + a ni a nn a 11 a 1i a 1n a 21 a 2i a 2n = a n1 a ni a nn a 11 a 1i a 1n a 21 a 2i a 2n + a n1 a ni a nn 5 Εστω A M n n (R) (αʹ) det(a) 0 αν και μόνον αν οι γραμμές (αντίστοιχα, οι στήλες) του A είναι γραμμικώς ανεξάρτητες (βʹ) det(a t ) = det(a) 6 Αν A, B M n n (R), τότε det(a B) = det(a) det(b) Πόρισμα 251 Η ορίζουσα ενός πίνακα που έχει δύο γραμμές ή δύο στήλες ίδιες ισούται με μηδέν 26 AneÔresh tou antðstrofou pðnaka Θεωρούμε έναν τετραγωνικό πίνακα: a 11 a 12 a 1n a 21 a 22 a 2n A = M n n(r) a n1 a n2 a nn Αντικαθιστώντας κάθε στοιχείο a ij με το αλγεβρικό του συμπλήρωμα, παίρνουμε τον πίνακα : A 11 A 12 A 1n A 21 A 22 A 2n M n n(r) A n1 A n2 A nn Ο συμπληρωματικός ή προσαρτημένος πίνακας του πίνακα A καλείται ο πίνακας: t A 11 A 12 A 1n A 11 A 21 A n1 A 21 A 22 A 2n A 12 A 22 A n2 adj(a) = = A n1 A n2 A nn A 1n A 2n A nn Θεώρημα 261 Αν ο πίνακας A είναι τετραγωνικός και det(a) 0, τότε A 1 = 1 det(a) adj(a)
28 26 Παραδείγματα Να βρεθεί ο αντίστροφος πίνακας τού ( ) t A11 A Εχουμε adj(a) = 12 = A 21 A 22 Άρα, ( 2 3 A = 4 5 ) t = ( Να βρεθεί ο αντίστροφος πίνακας τού A = Βρίσκουμε det(a) = 1 και adj(a) = Άρα, ) ( ( ) A = t = A 1 1 = det(a) adj(a) = 27 Prosdiorismìc tou bajmoô enìc pðnaka ) και det(a) = t = Για έναν πίνακα A = (a ij ) M m n (R) συμβολίζουμε με M j1jq i 1i p τον πίνακα που προκύπτει από τον A μετά τη διαγραφή των i 1 -γραμμής,, i p -γραμμής και j 1 -στήλης,, j q -στήλης Ο πίνακας M j1jq i 1i p καλείται ελλάσων πίνακας ή υποπίνακας του πίνακα A Θεώρημα 271 Ο βαθμός rank(a) ενός πίνακα A ισούται με το μέγιστο πλήθος των γραμμών του τετραγωνικού υποπίνακα του A με ορίζουσα διάφορη του μηδενός Παράδειγμα 271 Να βρεθεί ο βαθμός του πίνακα: A = Επειδή ο A είναι μη μηδενικός και έχει 4 γραμμές, 1 rank(a) 4 Παρατηρούμε ότι οι γραμμές του πίνακα είναι γραμμικώς εξαρτημένες, αφού A 4 = 2A 1 Άρα, rank(a) 3 Για τον πίνακα M4 4 = που προκύπτει από τον A μετά τη διαγραφή της 4ης γραμμής και της ης στήλης έχουμε: det(m4 4 ) = 4 0 Άρα, rank(a) = 3
29 27 28 Ask seic 17 Να βρεθεί το πλήθος των παραβάσεων στις παρακάτω μεταθέσεις και να χαρακτηριστούν οι μεταθέσεις ως άρτιες ή περιττές: ( ), 18 Να βρεθεί η ορίζουσα του πίνακα A = 19 Να βρεθούν οι ορίζουσες: ( , 20 Να βρεθούν οι ορίζουσες των πινάκων: , , , Να αποδειχθεί ότι: 22 Να αποδειχθεί ότι: a b c d a 2 b 2 c 2 d 2 a 3 b 3 c 3 d 3 23 Να βρεθούν οι ρίζες της εξίσωσης: ), ( ) με ανάπτυξη κατά τα στοιχεία της 2ης γραμμής = (b a)(c a)(d a)(c b)(d b)(d c) 1 + a a b 1 = a 2 b b 3 λ λ λ = 0 24 Να αποδειχθεί ότι σε ένα τετραγωνικό πίνακα A M n n (R) το άθροισμα των γινομένων των στοιχείων μιας στήλης (γραμμής) επί τα αλγεβρικά συμπληρώματα των αντίστοιχων στοιχείων μιας άλλης στήλης (γραμμής) είναι μηδέν, δηλαδή αν i j, τότε a 1i A 1j + + a ni A nj = 0 b 1 Λύση Εστω A = (A 1 A i A j A n ) Αντικαθιστώντας την j-στήλη με μια στήλη b = παίρνουμε τον πίνακα B = (A 1 A i b A n ) Αναπτύσσοντας την ορίζουσα του B κατά τη j-στήλη παίρνουμε det(b) = b 1 A 1j + + b n A nj Επειδή η ορίζουσα ενός πίνακα δεν αλλάζει όταν σε μία στήλη του προσθέτουμε μία άλλη, έχουμε b n det(b) = (b 1 + a 1i )A 1j + + (b n + a ni )A nj Επομένως det(b) = det(b) + a 1i A 1j + + a ni A nj Άρα, a 1i A 1j + + a ni A nj = 0
30 28 25 Να σχολιαστεί γιατί οι ορίζουσες είναι ίσες με μηδέν: , , a x 0 k b y 0 l c w 0 m d z 0 n, a 1 a 2 a 3 a 4 x 1 x 2 x 3 x 4 3a 1 3a 2 3a 3 3a Να υπολογιστεί ο βαθμός των πινάκων με τη χρήση των υποπινάκων (Θεώρημα 271): 27 Αν (i) (ii) a b c d e f g h i 2a c 2b 3c 2d f 2e 3f 2g i 2h 3i (iii) d e f a b c 3g 3h 3i , = 3, να υπολογιστούν οι ορίζουσες: 2a 3a + g d 2b 3b + h e 2c 3c + i f 28 Να αποδειχθεί ότι: (i) det(a t ) = det(a) (ii) Αν A t = A και το πλήθος των γραμμών του A είναι 2n + 1, τότε ο A είναι μη αντιστρέψιμος (iii) Ενας τετραγωνικός πίνακας A είναι μη αντιστρέψιμος αν και μόνον αν det(a) = 0 29 Να υπολογιστεί ο αντίστροφος του A εφαρμόζοντας τον τύπο A 1 = 1 det(a) adj(a): (i) A = , (ii) A = ( ) , (iii) A =
31 Kefˆlaio 3 EpÐlush susthmˆtwn grammik n exis sewn Σύστημα γραμμικών εξισώσεων με k - εξισώσεις και με n - αγνώστους είναι ένα σύστημα της μορφής: a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a k1 x 1 + a k2 x a kn x n = b k (31) Οι μεταβλητές x 1, x 2,, x n, οι συντελεσές a ij και οι σταθεροί (ελεύθεροι) όροι b i παίρνουν τιμές από το σύνολο των πραγματικών αριθμών R Κάθε n-διάστατο διάνυσμα (x 1, x 2,, x n ) με συντεταγμένες από το R, οι οποίες επαληθεύουν το σύστημα (31), καλείται λύση του συστήματος Ενα σύστημα γραμμικών εξισώσεων καλείται συμβατό, όταν έχει τουλάχιστον μία λύση Ενα σύστημα γραμμικών εξισώσεων καλείται τετραγωνικό, όταν το πλήθος των εξισώσεων ισούται με το πλήθος των αγνώστων Δύο συστήματα γραμμικών εξισώσεων καλούνται ισοδύναμα, όταν έχουν το ίδιο σύνολο λύσεων Σε κάθε σύστημα γραμμικών εξισώσεων της μορφής (31) μπορούμε να αντιστοιχίσουμε τρεις πίνακες: τον πίνακα συντελεστών τον πίνακα σταθερών όρων a 11 a 12 a 1n a 21 a 22 a 2n A = a k1 a k2 a kn b 1 b 2 b = (32) (33) b k και τον επαυξημένο πίνακα A b = a 11 a 12 a 1n a 21 a 22 a 2n a k1 a k2 a kn b 1 b 2 b k (34) 29
32 30 Δεδομένου ενός επαυξημένου πίνακα A b με k γραμμές και n + 1 στήλες, μπορεί να γραφεί σύστημα k εξισώσεις και με n αγνώστους της μορφής (31) Παράδειγμα 301 Στο σύστημα 3 γραμμικών εξισώσεων με 3 αγνώστους 3x 1 + x 2 + 2x 3 = 5 x 1 + 2x 2 + 4x 3 = 7 x 1 + 3x 2 + x 3 = 4 αντιστοιχούν ο πίνακας συντελεστών και ο επαυξημένος πίνακας A = και A b = EpÐlush tetragwnikoô sust matoc me th qr sh twn pinˆkwn Ενα σύστημα n γραμμικών εξισώσεων με n αγνώστους a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a n1 x 1 + a n2 x a nn x n = b n (35) μπορει να γραφεί σε μορφή πινάκων ως εξής A X = b, (36) όπου a 11 a 12 a 1n a 21 a 22 a 2n A =, X = a n1 a n2 a nn x 1 x 2 x n b 1, b = b 2 Άν ο πίνακας A είναι αντιστρέψιμος, τότε πολλαπλασιάζοντας την εξίσωση (36) με A 1 από αριστερά παίρνουμε διαδοχικά: A 1 A X = A 1 b = I X = A 1 b = X = A 1 b b n 32 EpÐlush sust matoc me apaloif agn stwn (Mèjodoc Gauss) Η μέθοδος Gauss επίλυσης συστήματος γραμμικών εξισώσεων με απαλοιφή αγνώστων βασίζεται στο παρακάτω θεώρημα: Θεώρημα 321 Άν οι πίνακες a 11 a 12 a 1n a 21 a 22 a 2n A b = a k1 a k2 a kn b 1 b 2 b k και C d = c 11 c 12 c 1n c 21 c 22 c 2n c j1 c j2 c jn d 1 d 2 d j είναι γραμμοϊσοδύναμοι, τότε είναι ισοδύναμα και τα αντίστοιχα συστήματα γραμμικών εξισώσεων: a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a k1 x 1 + a k2 x a kn x n = b k c 11 x 1 + c 12 x c 1n x n = d 1 c 21 x 1 + c 22 x c 2n x n = d 2 c j1 x 1 c j2 x 2 c jn x n = d j
33 31 Για να λύσουμε το σύστημα a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a k1 x 1 + a k2 x a kn x n = b k (37) ακολουθούμε τα παρακάτω βήματα 1 Γράφουμε τον επαυξημένο πίνακα A b = a 11 a 12 a 1n a 21 a 22 a 2n a k1 a k2 a kn 2 Φέρνουμε τον επαυξημένο πίνακα A b του συστήματος σε κλιμακωτή μορφή Â b Από το Θεώρημα 321 τα συστήματα γραμμικών εξισώσεων που αντιστοιχούν στους πίνακες A b και  b είναι ισοδύναμα 3 Υπάρχουν τρία ενδεχόμενα (αʹ) Ο Â έχει n μη μηδενικές γραμμές, δηλαδή a 11 0, a 22 0,, a nn 0, τότε ο  b έχει τη μορφή: Στην περίπτωση αυτή, b 1 b 2 b k â 11 â 12 â 13 â 1 n 1 â 1n 0 â 22 â 23 â 2 n 1 â 2n 0 0 â 33 â 3 n 1 â 3n  b = â n 1 n 1 â n 1 n â nn rank(a) = rank(a b) = n ˆb1 ˆb2 ˆb3 ˆbn 1 ˆbn Στο  b αντιστοιχεί το σύστημα â 11 x 1 + â 12 x 2 + â 13 x â 1n 1 x n 1 + â 1n x n = ˆb 1 â 22 x 2 + â 23 x â 2n 1 x n 1 + â 2n x n = ˆb 2 â n 1n 1 x n 1 + â n 1n x n = ˆb n 1 â nn x n = ˆb n Από την τελευταία εξίσωση βρίσκουμε x n = ˆb n â nn ˆbn ˆbn 1 â n 1n â Αντικαθιστώντας x n στην προτελευταία εξίσωση βρίσκουμε x n 1 = nn â n 1n 1 Ανεβαίνοντας προς τα πάνω βρίσκουμε διαδοχικά όλους τους αγνώστους Το σύστημα, στην περίπτωση αυτή, έχει μοναδική λύση
34 32 (βʹ) Το πλήθος k των μη μηδενικών γραμμών του  ισούται με το πλήθος των γραμμών του  b και k < n Τότε, ο  b έχει τη μορφή: 0 0 â 1i1 â 1n ˆb â 2i2 â 2n ˆb2  b = â kik â kn ˆbk (38) Στην περίπτωση αυτή, rank(a) = rank(a b) = k < n Οι μεταβλητές x i1, x i2,, x ik που αντιστοιχούν στα ηγετικά στοιχεία του κλιμακωτού πίνακα (38) καλούνται κύριες μεταβλητές, οι υπόλοιπες μεταβλητές καλούνται ελεύθερες Για απλούστευση της γραφής υποθέτουμε ότι τα ηγετικά στοιχεία των γραμμών του  είναι τα â 11, â 22,, â kk Τότε το αντίστοιχο στο  b σύστημα μπορεί να πάρει τη μορφή: â 11 x 1 + â 12 x â 1k x k = ˆb 1 a 1k+1 x k+1 a 1n x n â 22 x â 2k x k = ˆb 2 a 2k+1 x k+1 a 2n x n â kk x k = ˆb k a kk+1 x k+1 a kn x n (39) Οι μεταβλητές x 1, x 2,, x k στο σύστημα (39) είναι οι κύριες Δίνουμε στις ελεύθερες μεταβλητές του (39) αυθαίρετες τιμές Τότε παίρνουμε το σύστημα x k+1 = µ k+1, x k+2 = µ k+2,, x n = µ n â 11 x 1 + â 12 x â 1n x n = δ 1 â 22 x â 2k x k = δ 2 â kk x k = δ k το οποίο ως προς κύριες μεταβλητές έχει μοναδική λύση x 1 = µ 1, x 2 = µ 2,, x k = µ k Η λύση του αρχικού συστήματος θα είναι το n-διάστατο διάνυσμα (µ 1,, µ n ), οι συντεταγμένες του οποίου εξαρτώνται από τις αυθαίρετες τιμές των ελεύθερων μεταβλητών Το σύστημα, στην περίπτωση αυτή, έχει άπειρο πλήθος λύσεων (γʹ) Το πλήθος k των μη μηδενικών γραμμών του  είναι μικρότερο από το πλήθος των γραμμών του  b, δηλαδή το ηγετικό στοιχείο της τελευταίας γραμμής του  b βρίσκεται στη στήλη b Τότε ο  b έχει την μορφή 0 0 â 1i1 â 1n â 2i2 â 2n  b = a kik a kn Στην περίπτωση αυτή rank(a) = k < k + 1 = rank(a b) ˆb1 ˆb2 ˆbk ˆbk+1 0 0
35 33 Στην τελευταία μη μηδενική γραμμή του πίνακα αντιστοιχεί η εξίσωση 0 x x k+1 = ˆb k+1 0, η οποία είναι αδύνατη Το σύστημα, στην περίπτωση αυτή, δεν έχει λύση Πόρισμα 321 Εστω ότι A είναι ο πίνακας συντελεστών και ο A b είναι ο επαυξημένος πίνακας ενός συστήματος γραμμικών εξισώσεων με n αγνώστους Τότε 1 Το σύστημα είναι συμβατό rank(a) = rank(a b) 2 Το σύστημα έχει μοναδική λύση rank(a) = rank(a b) = n Παραδείγματα Να λυθεί το σύστημα Εχουμε A b = A 3+A A3 A x+ y+ z = 1 x+ 2y+ z = 1 x+ y+ 2z = Επομένως z = 3, y = 5 + z = 2 και x = 4 y 2z = 0 Άρα, (0, 2, 3) είναι η μοναδική λύση του συστήματος 2 Να λυθεί το σύστημα Εχουμε A b = A 3+2A x 4y + 5z = A3 2A1 A 1 2 A 1 x+ y+ 2z = 4 y z = 5 4z = x 6y + 4z = 2 4x 8y + 17z = 9 2A2 3A1 2A 3 4A 1 Άρα, το σύστημα έχει άπειρες λύσεις (2y 2, y, 1) x 4y+ 5z = 1 7z = 7 x = y 5 2 z = 2y 2 z = 1 3 Να λυθεί το σύστημα Εχουμε A b = A3 A1 A 2 A 1 x+ y+ z = 1 x+ y+ z = 1 x+ y+ z = Η τελευταία εξίσωση είναι αδύνατη Άρα, το σύστημα δεν έχει λύση x+ y+ z = 1 0 x+ 0 y+ 0 z = 2
36 34 33 EpÐlush sust matoc me ton kanìna tou Cramer Θεωρούμε ένα σύστημα n γραμμικών εξισώσεων με n αγνώστους a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a n1 x 1 + a n2 x a nn x n = b n (310) Συμβολίζουμε a 11 a 12 a 1n a 21 a 22 a 2n A = a n1 a n2 a nn και a 11 a 1 i 1 b 1 a 1 i+1 a 1n a 21 a 2 i 1 b 2 a 2 i+1 a 2n A xi =, i = 1,, n a n1 a n i 1 b n a n i+1 a nn Ο πίνακας A xi προκύπτει από τον πίνακα A με αντικατάσταση της i-στήλης του A με την στήλη b των ελεύθερων όρων Θεώρημα 331 (Κανόνας του Cramer) Αν det(a) 0, τότε το σύστημα (310) έχει μοναδική λύση (x 1, x 2,, x n ), όπου για κάθε i = 1,, n το x i βρίσκεται από τον τύπο: x i = det(a x i ) det(a) Παραδείγματα 331 Να λυθεί το σύστημα 3x + 4y + 2z = 5 5x 6y 4z = 3 4x + 5y + 3z = 1 Εχουμε det(a) = det(a y ) = = 12, det(a x) = = 24, det(a z) = = 12 = 60 Το σύστημα έχει μοναδική λύση x = det(a x) det(a) = 1, y = det(a y) det(a) = 2, z = det(a z) det(a) = 5
37 35 34 Omogen sust mata grammik n exis sewn Ορισμός 341 Ενα σύστημα γραμμικών εξισώσεων καλείται ομογενές αν όλοι οι ελεύθεροι όροι του είναι ίσοι με μηδέν Κάθε ομογενές σύστημα: a 11 x 1 + a 12 x a 1n x n = 0 a 21 x 1 + a 22 x a 2n x n = 0 a k1 x 1 + a k2 x a kn x n = 0 (311) είναι συμβατό, αφού η n-άδα (x 1,, x n ) = (0,, 0) ικανοποιεί όλες τις εξισώσεις του Συνθήκες κατά τις οποίες ένα ομογενές σύστημα n εξισώσεων με n αγνώστους έχει μη μηδενική λύση Από τον κανόνα του Cramer προκύπτει ότι η μηδενική λύση (x 1,, x n ) = (0,, 0) είναι η μοναδική του ομογενούς συστήματος με n εξισώσεις και n αγνώστους: a 11 x 1 + a 12 x a 1n x n = 0 a 21 x 1 + a 22 x a 2n x n = 0 a n1 x 1 + a n2 x a nn x n = 0 (312) αν και μόνον αν a 11 a 12 a 1n a 21 a 22 a 2n 0 a n1 a n2 a nn Πόρισμα 342 Το ομογενές σύστημα n γραμμικών εξισώσεων με n αγνώστους (312) έχει μη μηδενική λύση αν και μόνον αν η ορίζουσα των συντελεστών του είναι ίση με το μηδέν Δηλαδή, a 11 a 12 a 1n a 21 a 22 a 2n = 0 a n1 a n2 a nn
38 36 35 Ask seic 30 Να λυθούν τα παρακάτω συστήματα εξισώσεων: (i) x + z = c 1 x + y + z = c 2, z = c 3 z + w = c 4 (ii) x + 2y + z = 1 x + y + 2z = 4 (iii) x 1 + x 2 + 2x 3 + 3x 4 = 1 3x 1 x 2 x 3 2x 4 = 4 2x 1 + 3x 2 x 3 x 4 = 6 x 1 + 2x 2 + 3x 3 x 4 = 4 (iv) x 1 + 2x 2 + 4x 3 = 31 5x 1 + x 2 + 2x 3 = 29 3x 1 x 2 + x 3 = Να λυθεί το σύστημα AX = b, όπου A = 4 1 2, X = Να διερευνηθούν τα παρακάτω συστήματα εξισώσεων: (i) ax + y + z = 1 x + ay + z = 1 x + y + az = 1 33 Να λυθούν τα συστήματα με τον κανόνα του Cramer: (i) x + 2y + z = 1 2x 3y 2z = 1 x y + z = 4 34 Να βρεθεί το λ για το οποίο το σύστημα έχει λύση 2x 1 x 2 + x 3 + x 4 = 1 x 1 + 2x 2 x 3 + 4x 4 = 2 x 1 + 7x 2 4x x 4 = λ,, x 1 x 2 x 3, b = (ii) ax + y + z = 1 x + ay + z = a, x + y + az = a 2 (ii) x + y + 2z = 1 2x y + 2z = 4 4x + y + 4z = 2, 35 Να διερευνηθεί ποιά από τα παρακάτω συστήματα έχουν μη μηδενικές λύσεις: (i) 2x 3y + 4z w = 0 7x + y 8z + 9w = 0 2x + 8y + z w = 0 (iii) a 1 x + a 2 y + a 3 z = 0 b 1 x + b 2 y + b 3 z = 0 (ii) x + 3y z = 0 y 8z = 0 4z = 0 (iv) 3x 2y = 0 6x 4y = 0 36 Να βρεθούν οι τιμές του λ για τις οποίες οι ευθείες: x + 2y = 1, 2x + (1 λ)y = 1, (1 λ)x + 3y = 2 έχουν μόνο ένα κοινό σημείο και να βρεθεί το σημείο αυτό
39 37 37 Με τη μέθοδο απαλοιφής του Gauss να βρεθεί ο αντίστροφος του πίνακα A (i) A = Λύση (i) Θεωρούμε το σύστημα AX = b: Με τη μέθοδο απαλοιφής αγνώστων βρίσκουμε (ii) A = x 1 + 2x 2 + 3x 3 + 4x 4 = b 1 x 2 + 2x 3 + 3x 4 = b 2 x 3 + 2x 4 = b 3 x 4 = b Παρατηρούμε ότι Ομως X = A 1 b Άρα, x 1 = b 1 2b 2 + b 3 = 1 b 1 2 b b b 4 x 2 = b 2 2b 3 + b 4 = 0 b b 2 2 b b 4 x 3 = b 3 2b 4 = 0 b b b 3 2 b 4 x 4 = b 4 = 0 b b b b 4 x 1 x 2 x 3 x = A 1 = b 1 b 2 b 3 b 4
40 38
41 Mèroc II Analutik GewmetrÐa 39
42
43 Kefˆlaio 4 DianusmatikoÐ q roi Εστω E 3 ο τριδιάστατος Ευκλείδειος χώρος στον οποίο έχει οριστεί μία μονάδα μήκους Θεωρούμε δύο σημεία A και B του χώρου Συμβολίζουμε με AB το ευθύγραμμο τμήμα με άκρα A και B AB το μήκος του AB [AB) την ημιευθεία με αρχή το A η οποία διέρχεται από το B (AB) την ευθεία που διέρχεται απο τα σημεία A και B 41 Efarmostˆ dianôsmata tou q rou Ορισμός 411 Κάθε διατεταγμένο ζεύγος (A, B) σημείων A και B του χώρου (A το πρώτο σημείο του ζεύγος και B το δεύτερο σημείο του ζεύγος) καλείται εφαρμοστό διάνυσμα με αρχή το A και πέρας το B και συμβολίζεται με AB Ορισμός 412 Τα εφαρμοστά διανύσματα AB και CD λέγεται ότι έχουν την ίδια διέυθυνση αν και μόνον αν είτε (AB) = (CD) είτε (AB) (CD) Γράφουμε τότε AB CD Ορισμός 413 Δύο εφαρμοστά διανύσματα AB και CD που έχουν την ίδια διεύθυνση καλούνται ομόρροπα ή λέγεται ότι έχουν την φόρα (γράφουμε τότε AB CD) αν και μόνον αν (i) είτε τα σημεία A, B, C, D ανήκουν σε μία ευθεία και οι ημιευθείες [AB) και [CD) τέμνονται κατά μία ημιευθεία, (ii) είτε οι ευθείες (AB) και (CD) είναι παράλληλες και οι ημιευθείες [AB) και [CD) περιέχονται στο ίδιο ημιεπίπεδο ως προς την ευθεία (AC) Ορισμός 414 Δύο εφαρμοστα διανύσματα AB και CD που έχουν την ίδια διεύθυνση και δεν είναι ομόρροπα καλούνται αντίρροπα (γράφουμε AB CD) Ορισμός 415 Τα εφαρμοστά διανύσματα AB και CD καλούνται ίσα (γραφουμε AB = CD) όταν AB CD και AB = CD Πρόταση 416 Για κάθε εφαρμοστό διάνυσμα AB και για κάθε σημείο C υπάρχει μοναδικό σημείο D τέτοιο ώστε AB = CD Ορισμός 417 Εστω AB ένα εφαρμοστό διάνυσμα, ε μια ευθεία και π ένα επίπεδο (a) AB ε ( AB είναι παράλληλο στη ε) (AB) ε ή (AB) = ε (b) AB π ( AB είναι παράλληλο στο π) (AB) π ή (AB) π 41
44 42 ΚΕΦΑΛΑΙΟ 4 42 EleÔjera dianôsmata Πρόταση 421 Η ισότητα των εφαρμοστών διανυσμάτων είναι σχέση ισοδυναμίας στο σύνολο όλων των εφαρμοστών διανυσμάτων του χώρου, δηλαδή ικανοποιεί τα ακόλουθα αξιώματα: (i) AB = CD ανακλαστική ιδιότητα (ii) AB = CD = CD = AB συμμετρική ιδιότητα (iii) AB = CD και CD = EZ = AB = EZ μεταβατική ιδιότητα Ορισμός 422 Κάθε κλάση ισοδυναμίας ως προς τη σχέση ισοδυναμίας = στο σύνολο των εφαρμοστών διανυσμάτων του χώρου καλείται ελεύθερο διάνυσμα Τα ελεύθερα διανύσματα συμβολίζουμε με a, b, u, κτλ Συμβολίζουμε με 0 το ελεύθερο διάνυσμα που περιέχει τα εφαρμοστά διανύσματα: AA, BB, CC, κτλ Πρόταση 423 Για κάθε διάνυσμα u και για κάθε σημείο A υπάρχει μοναδικό σημείο B τέτοιο ώστε AB u Ορισμός 424 Εστω u και v δύο ελεύθερα διανύσματα, ε μια ευθεία του χώρου και π ένα επίπεδο του χώρου (a) u v ( u και v είναι παράλληλα) AB CD, όπου AB u και CD v (b) u ε ( u είναι παράλληλο στη ε) AB ε, όπου AB u (c) u π ( u είναι παράλληλο στο π) AB π, όπου AB u (d) u, v, w είναι συνεπίπεδα αν υπάρχει επίπεδο π τέτοιο ώστε u π, v π και w π Θεωρούμε ότι 0 u, 0 ε και 0 π Παρατήρηση 425 Για οποιαδήποτε ελεύθερα διανύσματα u και v υπάρχει επίπεδο π τέτοιο ώστε u π και v π Άθροισμα δυο ελεύθερων διανυσμάτων Το άθροισμα δυο ελεύθερων διανυσμάτων u και v ορίζεται ως εξής: (i) Παίρνουμε ένα τυχαίο σημείο A του χώρου (ii) Υπάρχει μοναδικό σημείο B τέτοιο ώστε AB u (iii) Υπάρχει μοναδικό σημείο C τέτοιο ώστε BC v Το ελεύθερο διάνυσμα που περιέχει το AC καλείται άθροισμα των u και v και συμβολίζεται με u + v Γινόμενο πραγματικού αριθμού επί ελεύθερο διάνυσμα Το γινόμενο ενός ελεύθερου διανύσματος u 0 επί λ R ορίζεται ως εξής: θεωρούμε AB u και ένα σημείο C της ευθείας (AB) τέτοιο ώστε (i) AC = λ AB (ii) AC AB, αν λ > 0, (iii) AC AB, αν λ < 0, (iv) C = A, αν λ = 0 Το ελεύθερο διάνυσμα που περιέχει το AC καλείται γινόμενο του λ επί του u και συμβολίζεται λ u ή με λ u Ορίζουμε λ 0 = 0, για κάθε λ R
45 DianusmatikoÐ q roi H ènnoia tou dianusmatikoô q rou Ορισμός 431 Εστω V ένα σύνολο και έστω ότι για κάθε u, v V έχει οριστεί στοιχείο u + v V και για κάθε u V, λ R έχει οριστεί στοιχείο λ u V Το σύνολο V μαζί με τις πράξεις + και καλείται διανυσματικός χώρος πάνω στο R, αν 1 u + v = v + u 2 ( u + v) + w = u + ( v + w) 3 0 V, τέτοιο ώστε u + 0 = u, u V, 4 u V, u V, τέτοιο ώστε u + ( u) = 0, 5 (λ + µ) u = λ u + µ u, λ, µ R, u V, 6 λ(µ u) = (λµ) u, λ, µ R, u V, 7 λ( u + v) = λ u + λ v, 8 1 u = u Το στοιχείο 0 με την ιδιότητα (3) καλείται ουδέτερο στοιχείο του V Για κάθε u V το στοιχείο u με την ιδιότητα (4) καλείται αντίθετο του u Θεώρημα 432 Το σύνολο V 3 όλων των ελεύθερων διανυσμάτων του Ευκλείδιου χώρου είναι διανυσματικός χώρος πάνω στο R Θεώρημα 433 Το σύνολο V π όλων των ελεύθερων διανυσμάτων παράλληλων σ ένα επίπεδο π είναι διανυσματικός χώρος πάνω στο R Θεώρημα 434 Το σύνολο V ε όλων των ελεύθερων διανυσμάτων παράληλων σε μια ευθεία ε είναι διανυσματικός χώρος πάνω στο R Θεώρημα 435 Για κάθε διανυσματικό χώρο (V, +, ) ισχύουν οι ακόλουθες ιδιότητες: (i) Το ουδέτερο στοιχεό 0 είναι μοναδικό (ii) Για κάθε u V το αντίθετο στοιχείο u είναι μοναδικό (iii) 0 u = 0 για κάθε u V (iv) λ 0 = 0 για κάθε λ R (v) u = ( 1) u για κάθε u V (vi) λ u = λ = 0 ή u = 0 44 Grammik exˆrthsh stoiqeðwn dianusmatikoô q rou Η προσεταιριστική ιδιότητα της πρόσθεσης των στοιχείων ενός διανυσματικού χώρου μας επιτρέπει να μιλάμε για το άθροισμα των τριών διανυσμάτων: u + v + w = ( u + v) + w = u + ( v + w) Με επαγωγή ορίζεται το άθροισμα οποιουδήποτε αριθμού διανυσμάτων: u 1 + u u n = ( u 1 + u u n 1 ) + u n Από τις ιδιότητες του διανυσματικού χώρου προκύπτει ότι μπορούμε να απλοποιούμε τις εξισώσεις και της παραστάσεις που περιέχουν διανύσματα-στοιχεία διανυσματικού χώρου όπως και τις εξισώσεις και τις παραστάσεις που περιέχουν μόνο αροιθμούς: να τοποθετούμε παρενθέσεις, να ανετιμεταθέτουμε τους όρους ενός α- θροίσματος, να μεταφέρουμε τους όρους από ένα μέλος μιας ισότητας στο άλλο αλλάζοντας πρόσημο
46 44 ΚΕΦΑΛΑΙΟ 4 Ορισμός 441 Εστω ότι u 1,, u n είναι στοιχεία ενός διανυσματικού χώρου V πάνω στο R Κάθε άθροισμα της μορφής λ 1 u λ n u n καλείται γραμμικός συνδυασμός των στοιχείων u 1,, u n με συντελεστές λ 1,, λ n Προφανώς κάθε γραμμικός συνδυασμός λ 1 u 1 ++λ n u n των στοιχείων u 1,, u n ενός διανυσματικού χώρου V είναι στοιχείο του V Για κάθε πεπερασμένο σύνολο σύνολο u 1,, u n στοιχείων ενός διανυσματικού χώρου V υπάρχουν λ 1,, λ n R τέτοιοι ώστε λ 1 u λ n u n = 0 Πράγματι, αρκεί να θέσουμε λ 1 = = λ n = 0, οπότε 0 u λ n u n = 0 Ο γραμμικός συνδυασμός 0 u u n καλείται τετριμμένος γραμμικός συνδυασμός των u 1,, u n Ορισμός 442 Το διανύσματα u 1,, u n καλούνται γραμμικώς εξαρτημένα, αν υπάρχει μη τετριμμένος γραμμικός συνδυασμός αυτών ίσος με το διάνυσμα 0 Δηλαδή αν υπάρχουν λ 1,, λ n R τέτοιοι ώστε: (i) λ 1 u λ n u n = 0, (ii) λ λ n 0 Ορισμός 443 Το διανύσματα u 1,, u n καλούνται γραμμικώς ανεξάρτητα, αν ο μόνος γραμμικός συνδυασμός αυτών ίσος με το διάνυσμα 0 είναι ο τετριμμένος Δηλαδή Παραδείγματα Αν u 0, τότε u είναι γραμμικώς ανεξάρτητο λ 1 u λ n u n = 0 λ 1 = = λ n = 0 Πράγματι, αν λ u = 0, τότε επειδή u 0 είναι λ = 0 2 Αν u v, τότε u, v είναι γραμμικώς εξαρτημένα Πράγματι, (i) Αν u = 0, τότε 1 u + 0 v είναι μη τετριμμένος γραμμικός συνδυασμός των u και v ίσος με το 0 (ii)αν v = 0, τότε 0 u + 1 v είναι μη τετριμμένος γραμμικός συνδυασμός των u και v ίσος με το 0 (iii) Αν u και v είναι δύο μη μηδενικά παράλληλα διανύσματα, τότε u = λ v Άρα, 1 u λ v είναι μη τετριμμένος γραμμικός συνδυασμός των u και v ίσος με το 0 45 Basikèc protˆseic gia thn grammik exˆrthsh Εστω ότι u, u 1,, u n, u n+1 είναι στοιχεία ενός διανυσματικού χώρου πάνω στο R Πρόταση 451 Αν ένα από τα διανύσματα u 1,, u n είναι 0, τότε τα u 1,, u n είναι γραμμικώς εξαρτημένα Απόδειξη Εστω πχ u 1 = 0, τότε 1 u u u n = 0, όπου ο γραμμικός συνδυασμός 1 u u u n είναι μη τετριμμένος Πρόταση 452 Τα διανύσματα u 1,, u n είναι γραμμικώς εξαρτημένα τότε και μόνον τότε, όταν ένα από τα διανύσματα u 1,, u n είναι γραμμικός συνδυασμός των άλλων Πρόταση 453 Αν u 1,, u n είναι γραμμικώς ανεξάρτητα και u 1,, u n, u είναι γραμμικώς εξαρτημένα, τότε u είναι γραμμικός συνδυασμός των u 1,, u n Πρόταση 454 Αν τα u 1,, u n είναι γραμμικώς ανεξάρτητα και τότε οι αριθμοί λ 1,, λ n είναι μοναδικοί u = λ 1 u λ n u n, Πρόταση 455 Αν u 1,, u n, u n+1 είναι γραμμικώς ανεξάρτητα, τότε u 1,, u n είναι γραμμικώς ανεξάρτητα Πρόταση 456 Αν u 1,, u n είναι γραμμικώς εξαρτημένα, τότε u 1,, u n, u n+1 είναι γραμμικώς εξαρτημένα
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ. Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες,
 ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
ΠΛΗ 12- Σχέση ισοδυναμίας, γραμμικά συστήματα και απαλοιφή Gauss
 .4 Σχέση ισοδυναμίας, γραμμικά συστήματα και απαλοιφή Gauss Σχέση ισοδυναμίας. Έστω το σύνολο των ρητών αριθμών Q και η σχέση της ισότητας σε αυτό που ορίζεται ως εξής: Δύο στοιχεία α, γ Q είναι ίσα αν
.4 Σχέση ισοδυναμίας, γραμμικά συστήματα και απαλοιφή Gauss Σχέση ισοδυναμίας. Έστω το σύνολο των ρητών αριθμών Q και η σχέση της ισότητας σε αυτό που ορίζεται ως εξής: Δύο στοιχεία α, γ Q είναι ίσα αν
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
Κεφάλαιο 2 Πίνακες - Ορίζουσες
 Κεφάλαιο Πίνακες - Ορίζουσες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο 3 ο Τρίμηνο ο Τρίμηνο Είδος
Κεφάλαιο Πίνακες - Ορίζουσες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο 3 ο Τρίμηνο ο Τρίμηνο Είδος
0 + a = a + 0 = a, a k, a + ( a) = ( a) + a = 0, 1 a = a 1 = a, a k, a a 1 = a 1 a = 1,
 I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
Κ. Ι. ΠΑΠΑΧΡΗΣΤΟΥ. Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ. Ιδιότητες & Εφαρµογές
 Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
ΚΕΦΑΛΑΙΟ 2: ΟΡΙΖΟΥΣΕΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
[A I 3 ] [I 3 A 1 ].
![[A I 3 ] [I 3 A 1 ]. [A I 3 ] [I 3 A 1 ].](/thumbs/65/54189091.jpg) ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Εάν A = τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό. det( A) = = ( 2)4 3 1 = 8 3 = 11. τότε η ορίζουσά του πίνακα ισούται με
 Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
AX=B (S) A A X=A B I X=A B X=A B I X=A B X=A B X=A B X X
 . Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
. Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων. Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58
 Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων Τηλ. 26410741964196 E-mail fkoutel@cc.uoi.gr ΜΑΘΗΜΑΤΙΚΑ Ι ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58 Γραµµική άλγεβρα...... είναι τοµέας
Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων Τηλ. 26410741964196 E-mail fkoutel@cc.uoi.gr ΜΑΘΗΜΑΤΙΚΑ Ι ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58 Γραµµική άλγεβρα...... είναι τοµέας
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
2 3x 5x x
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Διανύσµατα στο επίπεδο
 Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου
Πίνακες Γραμμικά Συστήματα
 Πίνακες Γραμμικά Συστήματα 1. Είδη Πινάκων Οι πίνακες είναι ένα χρήσιμο μαθηματικό εργαλείο, με εφαρμογές και διασυνδέσεις σε πολλές επιστήμες. Η σημαντικότερη εφαρμογή των πινάκων είναι στην επίλυση συστημάτων
Πίνακες Γραμμικά Συστήματα 1. Είδη Πινάκων Οι πίνακες είναι ένα χρήσιμο μαθηματικό εργαλείο, με εφαρμογές και διασυνδέσεις σε πολλές επιστήμες. Η σημαντικότερη εφαρμογή των πινάκων είναι στην επίλυση συστημάτων
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ. ρ Χρήστου Νικολαϊδη
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
Ορισμοί και πράξεις πινάκων
 Ορισμοί και πράξεις πινάκων B.. Εισαγωγή Κατά την εύρεση των μαθηματικών μοντέλων των σύγχρονων δυναμικών συστημάτων, διαπιστώνεται ότι οι διαφορικές εξισώσεις που εμπλέκονται μπορούν να γίνουν πολύ περίπλοκες
Ορισμοί και πράξεις πινάκων B.. Εισαγωγή Κατά την εύρεση των μαθηματικών μοντέλων των σύγχρονων δυναμικών συστημάτων, διαπιστώνεται ότι οι διαφορικές εξισώσεις που εμπλέκονται μπορούν να γίνουν πολύ περίπλοκες
Πίνακες Ορίζουσες. Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες.
 1 Πίνακες Ορίζουσες Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες. Παράδειγμα (χορήγηση Βαλασικλοβιρης (αντιυπερτασικό) σε νήπια) Ηλικία (μήνες) Μέσο Cmax (μg/ml) Μέσο βάρος
1 Πίνακες Ορίζουσες Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες. Παράδειγμα (χορήγηση Βαλασικλοβιρης (αντιυπερτασικό) σε νήπια) Ηλικία (μήνες) Μέσο Cmax (μg/ml) Μέσο βάρος
Σημειώσεις για το μάθημα: «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α )
 Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
= 7. Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις
 1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 1. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 5 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 5 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Πίνακες και Γραμμικά Συστήματα: Ο Αλγόριθμος Guss Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Πίνακες και Γραμμικά Συστήματα: Ο Αλγόριθμος Guss Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
, ορίζουμε deta = ad bc. Πρόταση Ένας πίνακας Α είναι αντιστρέψιμος τότε και μόνο αν deta 0.
 Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
Μεταθέσεις και πίνακες μεταθέσεων
 Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης
 Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 12: Μήτρες (Θεωρία) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 12: Μήτρες (Θεωρία) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
x y z d e f g h k = 0 a b c d e f g h k
 Σύνοψη Κεφαλαίου 3: Προβολική Γεωμετρία Προοπτική. Εάν π και π 2 είναι δύο επίπεδα που δεν περνάνε από την αρχή O στο R 3, λέμε οτι τα σημεία P στο π και Q στο π 2 βρίσκονται σε προοπτική από το O εάν
Σύνοψη Κεφαλαίου 3: Προβολική Γεωμετρία Προοπτική. Εάν π και π 2 είναι δύο επίπεδα που δεν περνάνε από την αρχή O στο R 3, λέμε οτι τα σημεία P στο π και Q στο π 2 βρίσκονται σε προοπτική από το O εάν
7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7.2 ΜΗΤΡΕΣ ΕΙΔΙΚΗΣ ΜΟΡΦΗΣ (Ι)
 77 78 7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7. ΕΙΣΑΓΩΓΗ Η Άλγεβρα των μητρών οι πινάκων είναι ιδιαίτερα χρήσιμη για την επίλυση συστημάτων καθώς επίσης στις επιστήμες της οικονομετρίας και της στατιστικής. ΟΡΙΣΜΟΣ: Μήτρα
77 78 7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7. ΕΙΣΑΓΩΓΗ Η Άλγεβρα των μητρών οι πινάκων είναι ιδιαίτερα χρήσιμη για την επίλυση συστημάτων καθώς επίσης στις επιστήμες της οικονομετρίας και της στατιστικής. ΟΡΙΣΜΟΣ: Μήτρα
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
2x y = 1 x + y = 5. 2x y = 1. x + y = 5. 2x y = 1 4x + 2y = 0. 2x y = 1 4x + 2y = 2
 Σημειώσεις μαθήματος Μ22 Γραμμική Άλγεβρα Ι Βασισμένες στο βιβλίο του GStrang Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2 Εισαγωγή Αυτές οι σημειώσεις καλύπτουν την ύλη του μαθήματος
Σημειώσεις μαθήματος Μ22 Γραμμική Άλγεβρα Ι Βασισμένες στο βιβλίο του GStrang Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2 Εισαγωγή Αυτές οι σημειώσεις καλύπτουν την ύλη του μαθήματος
n! k! (n k)!, = k k 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jordan
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Ομογενή Συστήματα Ορισμός Ενα σύστημα λέγεται ομογενές αν όλοι οι σταθεροί όροι του (δηλαδή οι όροι του δεξιού μέλους του συστήματος) είναι μηδέν.
 Ομογενή Συστήματα Ορισμός Ενα σύστημα λέγεται ομογενές αν όλοι οι σταθεροί όροι του (δηλαδή οι όροι του δεξιού μέλους του συστήματος) είναι μηδέν. Ομογενή Συστήματα Ορισμός Ενα σύστημα λέγεται ομογενές
Ομογενή Συστήματα Ορισμός Ενα σύστημα λέγεται ομογενές αν όλοι οι σταθεροί όροι του (δηλαδή οι όροι του δεξιού μέλους του συστήματος) είναι μηδέν. Ομογενή Συστήματα Ορισμός Ενα σύστημα λέγεται ομογενές
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
= k. n! k! (n k)!, k=0
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
8.1 Διαγωνοποίηση πίνακα
 Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
1 Ορίζουσες. Άσκηση 1.1 Θεωρούμε τον πίνακα. 1 x x x x 1 x x x x 1 x x x x 1 A =
 1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
a 11 a 1n b 1 a m1 a mn b n
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 28/4/2014 ΧΚουρουνιώτης (ΠανΚρήτης) Διάλεξη 13 28/4/2014 1 / 14 Πίνακες πάνω από σώμα K Πίνακες πάνω από σώμα K Το σύνολο των m n
Γραμμική Άλγεβρα ΙΙ Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 28/4/2014 ΧΚουρουνιώτης (ΠανΚρήτης) Διάλεξη 13 28/4/2014 1 / 14 Πίνακες πάνω από σώμα K Πίνακες πάνω από σώμα K Το σύνολο των m n
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 1. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
2.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 .0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
Ιδιάζουσες τιμές πίνακα. y έχουμε αντίστοιχα τις σχέσεις : Αυτές οι παρατηρήσεις συμβάλλουν στην παραγοντοποίηση ενός πίνακα
 Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
Παναγιώτης Ψαρράκος Αν. Καθηγητής
 Ανάλυση Πινάκων Κεφάλαιο 2: Παραγοντοποίηση LU Παναγιώτης Ψαρράκος Αν Καθηγητής ΔΠΜΣ Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών Εθνικό Μετσόβιο
Ανάλυση Πινάκων Κεφάλαιο 2: Παραγοντοποίηση LU Παναγιώτης Ψαρράκος Αν Καθηγητής ΔΠΜΣ Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών Εθνικό Μετσόβιο
ΜΑΘΗΜΑΤΙΚΑ Ι Α ΜΕΡΟΣ
 ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι Περιληπτικές Σημειώσεις-Ασκήσεις Α ΜΕΡΟΣ ΦΩΤΟΥΛΑ ΑΡΓΥΡΟΠΟΥΛΟΥ ΚΑΘ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑΤΟΣ ΔΕΟ Msc Θεωρητικά Μαθηματικά ΚΑΛΑΜΑΤΑ 6 ΠΕΡΙΕΧΟΜΕΝΑ ΣΕΛ ΕΙΣΑΓΩΓΗ
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι Περιληπτικές Σημειώσεις-Ασκήσεις Α ΜΕΡΟΣ ΦΩΤΟΥΛΑ ΑΡΓΥΡΟΠΟΥΛΟΥ ΚΑΘ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑΤΟΣ ΔΕΟ Msc Θεωρητικά Μαθηματικά ΚΑΛΑΜΑΤΑ 6 ΠΕΡΙΕΧΟΜΕΝΑ ΣΕΛ ΕΙΣΑΓΩΓΗ
Ευκλείδειοι Χώροι. Ορίζουµε ως R n, όπου n N, το σύνολο όλων διατεταµένων n -άδων πραγµατικών αριθµών ( x
 Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
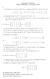 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
ΚΕΦΑΛΑΙΟ 2. Γραμμικοί Κώδικες. 2.1 Η έννοια του Γραμμικού κώδικα
 ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
t t Αν κάποιος από αυτούς είναι αντιστρέψιμος, υπολογίστε τον αντίστροφό του. 2. Υπολογίστε την ορίζουσα του Δείξτε τα εξής.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
Βάση και Διάσταση Διανυσματικού Χώρου
 Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 2004 Θέμα 1 ο. 4
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΙΙ ΜΑΘΗΜΑ 1-2-ΠΙΝΑΚΕΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΠΑΝΗΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΙΙ ΜΑΘΗΜΑ 1-2-ΠΙΝΑΚΕΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2010-2011 ΠΑΝΗΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΙΝΑΚΑΣ Ένας πίνακας Α με στοιχεία από το σύνολο F (συνήθως θεωρούμε τα σύνολα
ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΙΙ ΜΑΘΗΜΑ 1-2-ΠΙΝΑΚΕΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2010-2011 ΠΑΝΗΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΙΝΑΚΑΣ Ένας πίνακας Α με στοιχεία από το σύνολο F (συνήθως θεωρούμε τα σύνολα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Συστήματα Γραμμικών Εξισώσεων Εισαγωγή Σύστημα γραμμικών εξισώσεων a x a x a x b 11
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Συστήματα Γραμμικών Εξισώσεων Εισαγωγή Σύστημα γραμμικών εξισώσεων a x a x a x b 11
Gauss. x + y + z = 2 3x + 3y z = 6 x y + z = 1. x + y + z = r x y = 0 3x + y + sz = s 0
 Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ορίζουσες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Ορίζουσα H Ορίζουσα είναι ένας αριθμός και ορίζεται μόνον για τετραγωνικούς
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ορίζουσες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Ορίζουσα H Ορίζουσα είναι ένας αριθμός και ορίζεται μόνον για τετραγωνικούς
ΙΑΝΥΣΜΑΤΑ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. Τι ονοµάζουµε διάνυσµα; αλφάβητου επιγραµµισµένα µε βέλος. για παράδειγµα, Τι ονοµάζουµε µέτρο διανύσµατος;
 ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
